
Les fusées circulant dans le vide pour la majeure de leur trajet ( dès qu'elles ont quitté l'atmosphère ), leur principe de fonctionnement doit donc être adapté à ce type particulier de milieu, et faire appel à des modes de propulsion adéquates. Ainsi, les systèmes mis au point ne pouvant pas avoir d'échange avec le milieu extérieur, ils doivent fonctionner de manière complètement isolée et autonome, sans source d'énergie extérieure. Toute l'énergie consommée par la fusée au cours de sa mission devra donc être emportée par celle-ci depuis son départ, et donc depuis la Terre (ou de son autre lieu de décollage).
Le mode de propulsion actuel est basé sur l'éjection de matière ( de gaz ) à grande vitesse pour pouvoir fournir aux engins spatiaux l'accélération et la puissance nécessaire pour s'arracher à l'attraction terrestre. C'est encore le seul et unique moyen qui permet de quitter l'atmosphère terrestre, et il a été utilisé pour tous les lancements de sonde et mises en orbite de satellite, ainsi que pour les voyages vers la Lune.

L'éjection de gaz à grande vitesse reste le seul moyen efficace pour donner à la fusée la puissance nécessaire pour quitter l'atmosphère terrestre.
Pour expliquer le principe physique de cette propulsion, il faut directement faire appel au principe newtonien de l'action et de la réaction, qui affirme que dans un système pseudo-isolé, la somme des forces qui s'exercent sur un mobile à vitesse nulle ou à vitesse constante est égale à 0. En effet, pour un système isolé telle qu'une fusée dans l'espace ( pour modéliser ce système, l'espace sera considéré comme système pseudo-isolé, et l'on négligera les forces extérieures telles que les forces de gravitation des astres environnants ), la somme des forces ( intérieures donc) s'exerçant sur les différentes parties du système est nulle.
![]()
Si l'on souhaite considérer séparément les différentes parties du mobile et indépendantes de la fusée ( en fait la structure principale sans les gaz éjectés ), on peut affirmer que les forces intérieures au système { fusée }, c'est-à-dire { structure + gaz éjectés } sont en fait des forces extérieures pour chaque partie indépendante { structure } et { gaz éjectés }.
Pour exprimer la somme des forces extérieures pour un système donné, il faut ici faire appel au principe fondamental de la dynamique, qui s'énonce ainsi : dans un repère galiléen, la somme des forces qui s'exercent sur un point matériel de masse m est proportionnelle à son accélération.
En effet, la vitesse d'un point matériel est une grandeur vectorielle caractérisée par une direction, un sens, et une valeur numérique, sa norme. Lorsque le vecteur vitesse varie pendant un intervalle de temps donné, ces variations peuvent être plus ou moins importantes, et s'effectuer dans telle ou telle direction, dans un sens ou dans un autre. La variation dans le temps du vecteur vitesse est donc un vecteur, qui correspond à l'accélération. L'unité physique qui permet de mesurer l'intensité d'une accélération exprime par conséquent une variation de vitesse par unité de temps. Dans le système international (SI), c'est le mètre par seconde par seconde ou mètre par "seconde carrée".
Ainsi, le principe fondamental de la dynamique peut s'écrire :

Ainsi, on peut définir la somme des forces extérieures pour un système donné, d'après le principe fondamental de la dynamique, énoncé précédemment :
![]()
![]()
La quantité de mouvement d'un objet (q), qui est le produit de sa masse par sa vitesse a déjà été définie dans un paragraphe antérieure ( confer 1° partie, paragraphe I ).
dp = m x dv d'où (dp/dt) = m (dv/dt)
De plus (dv/dt)= a, où a représente l'accélération,
Donc (dp/dt)=ma
L'expression ci dessous traduit donc le principe de la loi 2 de Newton, qui nous montre que : Σ Fext = m x a
D’après ce qui précède on peut donc affirmer que:
![]()
Ces expressions traduisent donc un mouvement uniforme.
Ainsi, nous avons établi la conservation de la quantité de mouvement, qui permettra d'énoncer ultérieurement le principe de la propulsion.
Considérons une fusée de masse m et de vitesse V, la vitesse d’éjection des gaz étant W :
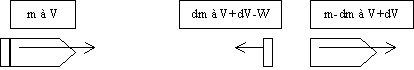
- au temps t : p = mV (définition de la quantité de mouvement )
- au temps t + dt : p = (m-dm)(V+dV)+dm(V+dV-W)
- dt est la dérivée en fonction du temps
- dm est la dérivée en fonction de la masse,
- dV est la dérivée en fonction de la vitesse,
- m-dm représente la diminution de la masse des combustibles,
- V+dV représente l'augmentation de la vitesse de la fusée,
- dm(V+dV-W) représente la vitesse d'éjection des gaz en fonction de la diminution de la masse des combustibles et de l'augmentation de la vitesse de la fusée. La vitesse d'éjection des gaz s'exprime sous la forme ( - W ) , car elle s'oppose à la quantité de mouvement, qui est une grandeur vectorielle de sens opposé à la vitesse d'éjection des gaz.
d’après le principe de conservation de la quantité de mouvement:
mV = (m-dm)(V+dV)+dm(V+dV-W) Û m dV = -W dm (1)
d'où: dV = -W dm/m
qui par intégration donne l’équation fondamentale de la propulsion par fusée:
![]()
Vo représentant les pertes par gravité et traînée aérodynamique.
On déduit de cette expression que l’accroissement de vitesse sera d’autant plus grand que:
- Le rapport entre masse initiale et masse finale sera plus élevé, ce qui impose donc de concevoir des réservoirs et structures porteuses les plus légers possibles.
- La vitesse d’éjection des gaz sera la plus grande: ici intervient la performance du moteur.
L’expression (1) obtenue précédemment a une grande importance puisqu’elle sert à définir la poussée, force caractérisant la performance d’un moteur.
En effet en divisant chaque membre par dt, on obtient:
![]()
La quantité m(dv/dt) représente ici la force de poussé, et on identifie le facteur dm/dt au débit massique de la fusée. On a également établi précédemment que (- w ) représente la vitesse d'éjection des gaz (elle est négative car elle s'oppose à la quantité de mouvement).
On a donc établi la formule de la poussée: F = q Ve
F : force de poussée ( F=(m(dv/dt) )
Ve : vitesse d’éjection
des gaz (Ve= -w)
q : débit massique ( q = dm/dt )
En réalité d’autres facteurs, comme la pression, interviennent dans cette expression et nous développerons donc l'expression de cette force ultérieurement.(cf partie tuyère).
Supposons que nous disposions de plusieurs moteurs identiques par leurs structures (forme et équipements) et leurs tuyères mais ayant des chargements réalisés avec des propergols différents. (ils ne brûlent pas les mêmes combustibles)
La comparaison de leurs performances peut se faire facilement en mesurant la poussée F délivrée par chacun d’eux pendant son fonctionnement. On peut donc comparer les différentes compositions de propergols utilisés en ramenant la poussée F obtenue au débit-poids du propergol consommé : on compare les performances des différents propergols utilisés en observant la masse de combustible utilisée pour obtenir une certaine poussée, et ceci sur un certain temps.
Pour un moteur donné, ce rapport, poussée délivrée sur débit poids, permet de caractériser le propergol utilisé. On le nomme impulsion spécifique du propergol. Il a les dimensions d’un temps et s’exprime en secondes.
![]()
- Is est l'impulsion spécifique du propergol.
- F est la
force de poussée.
- q est le débit-poids du propergol concerné, c'est à dire
sa capacité à produire une certaine énergie en fonction de sa masse, et cela
sur un certain temps.
- go désigne l'accélération dû
à la gravité à la surface de la Terre.