Appliquons le premier principe de la thermodynamique:
Q=ΔU+W
aux gaz éjectés par la tuyère:
Ec + D Ep + D U = Q + W
Ces gaz sont issus de la chambre de combustion où s’effectue la réaction à la pression Pc et à la température Tc .
Considérons les parois de la chambre de combustion adiabatique ( sans échanges de chaleur possible donc Q = 0) et les parois de la tuyère indéformables ( donc W = Wforces de pression).
On peut notamment négliger la variation d’énergie potentielle D Ep , si l’on considère qu’entre deux instants très proches la fusée sera à la même altitude.
Le premier principe s’écrit donc: D Ec + D U = Wforces de pression Û D Ec + D H = 0
car ΔU - Wforces de pression=ΔH
soit : ½ m (vf ² - vi ²) + m cp (Tf – Ti) = 0
où cp est la capacité calorifique massique à pression constante.
On peut négliger la vitesse d’injection des gaz dans la chambre de combustion, c'est-à-dire vi = 0 .
Si l’on suppose que la fusée est dans le vide, la température Ti est nulle, ce qui fait dès lors apparaître la formule de la vitesse limite d’éjection dans le vide:
![]()
Si l’on suppose par contre que la fusée évolue dans l’atmosphère, la température finale To des gaz éjectés est celle de l’air, de même que leur pression Po est égale la pression atmosphérique, d’où l’expression de la vitesse:
![]()
Or cp s’exprime à partir du rapport des capacités calorifiques g = cp /cv :
cp = g / (g - 1) x R / M
où M est la masse molaire du gaz en question et R est la constante des gaz parfaits (cf annexes Loi des gaz parfaits)
Ainsi on trouve en remplaçant :
![]()
On suppose alors la réaction adiabatique réversible, ce qui
nous permet d’utiliser la relation de Laplace qui dit que le long
d'une compression adiabatique(sans échange de chaleur) d'un gaz parfait, la
pression P et le volume V d'un gaz parfait sont reliés par PVg
= cte où g est le coefficient de compression adiabatique
ou isentropique égal au rapport g=Cp/Cv
des chaleurs spécifiques à pression constante et à volume constant.
( A température ambiante, g=5/3 pour un gaz
monoatomique et g est proche de 7/5 pour un gaz
diatomique.)
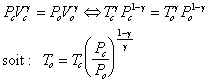
Ce qui aboutit finalement à la formule de la vitesse d’éjection des gaz suivante:
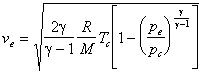
La vitesse d’éjection des gaz joue un rôle primordial dans le calcul de la poussée. Il est donc intéressant d’écrire sa formule complète (formule ci-dessus), car elle montre bien que cette vitesse augmente quand T0 augmente ou quand la masse molaire des gaz éjectés diminue.